The stabilizer trilogy II — Logical operators
Happy to see you back for the second part of the stabilizer trilogy! In the previous post, we defined stabilizer codes and gave a few examples of codes and constructions. In particular, we studied the Steane code, which can be defined by laying down seven qubits on a triangle with three colored faces, each representing an X and a Z stabilizer. However, we left pending a few important questions: what are the parameters of the code, and in particular the number of logical qubits and the distance? What logical operations can we apply to this code? How does the decoding process work?
In this post, we will get down to the nitty-gritty of logical operations. Those are unitary operators acting on the physical qubits, which allow you to go from one part of the codespace to another. For instance, a logical Hadamard lets you go from the logical zero state \vert 0 \rangle_L to the logical plus state \vert + \rangle_L. An important class of logical operations are the Pauli logicals, whose properties form a crucial component of stabilizer codes, as they allow to derive the distance of the code, the number of logical qubits, and the main formulation of decoding. Formalizing all those ideas rigorously relies on a fair bit of abstraction, using notions such as centralizers, normalizers, equivalence classes, etc. While we won’t shy away from the abstraction, we will also make every notion as concrete as possible using the Steane code as our running example.
We will start by showing how to count the number of logical qubits encoded in a stabilizer code. We will then formalize the notion of logical gates in a stabilizer code, and specialize the definition to the case of Pauli operators. Finally, we will see how to understand logical operators in terms of equivalent classes, which will become very handy when trying to understand decoding and topological constructions.
Logical qubits
Before exploring logical operations, let’s first understand how to count the logical qubits of a stabilizer code. Remember that the number of logical qubits is given by the logarithm of the dimension of the codespace. Indeed, if the codespace has dimension four, any logical state can be written as
\begin{aligned}
\vert \psi \rangle_L = a_1 \vert a_1\rangle + a_2 \vert a_2\rangle + a_3 \vert a_3\rangle + a_4 \vert a_4\rangle
\end{aligned}Relabelling \vert a_1\rangle as \vert 00\rangle_L, \vert a_2\rangle as \vert 01\rangle_L, etc. shows that the space corresponds to a two-qubit space.
So what we really need to compute is the dimension of \mathcal{C} for a stabilizer code.
Let n denote the number of physical qubits of our code, and m the number of generators of the stabilizer group (i.e. there are m independent elements whose products generate the whole group). The dimension of the codespace is then given by
\begin{aligned}
\text{dim}(\mathcal{C})=2^{n-m}
\end{aligned}and the number of logical qubits is therefore k=n-m. This should remind you of classical codes, where the same formula applies when m is the number of independent parity checks.
Intuitively, the argument goes as follow: the dimension of the physical Hilbert space is 2^n, and each independent constraint S_i \vert \psi \rangle = \vert \psi \rangle divides this dimension by two. For instance, let’s start with the full space and consider an arbitrary stabilizer S_i. It has two eigenvalues, +1 and -1, with the same multiplicity (since the trace of a Pauli operator is always zero), dividing the physical Hilbert space into two eigenspaces of equal dimension. We then need to show that the next stabilizer we choose divides this new space into two as well, etc. Let’s prove this rigorously through the following exercise.
Exercise 1: Let \Pi_{\mathcal{C}}=\frac{1}{2^m} (1+S_1)\ldots (I+S_m)
(a) Show that \Pi_{\mathcal{C}} is a projector onto the codespace, that is, \Pi_{\mathcal{C}} |\psi\rangle=|\psi\rangle if |\psi\rangle \in \mathcal{C}, and \Pi_{\mathcal{C}} |\psi\rangle=0 if |\psi\rangle \in \mathcal{C}^\perp.
(b) Show that we can rewrite this projector as \Pi_{\mathcal{C}}=\frac{1}{2^m}\sum_{S \in \mathcal{S}} S, where \mathcal{S} is the full stabilizer group.
(c) Show that \text{Tr}[\Pi_\mathcal{C}]=\text{dim}(\mathcal{C})
(d) Deduce that \text{dim}(\mathcal{C})=2^{n-m}
(solution)
Let’s apply this formula to the Steane code. As a reminder, the Steane code is a 7-qubit code defined on the following lattice, such that each face (also called plaquette) supports an X and a Z stabilizer generator:
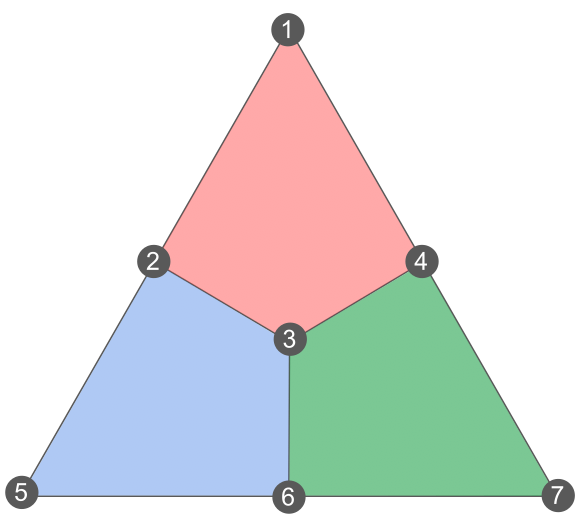
Therefore, the Steane code has six independent stabilizer generators, three X plaquettes and three Z plaquettes, such that m=6. Hence we can see that it encodes k=7-6=1 logical qubits.
Logical gates
Now that we know the number of encoded qubits, what about the distance?
To describe it, we need to introduce the notion of Pauli logical operator, which is a special case of logical gate. A logical gate is a unitary operator L that maps the codespace to itself,
i.e. such that L \vert \psi \rangle \in \mathcal{C} for all \vert \psi \rangle \in \mathcal{C}.
Logical gates therefore include stabilizers, but also operators that map one part of the codespace to another part.
For instance, a logical Hadamard maps the logical zero state \vert \overline{0} \rangle to the logical plus state \vert \overline{+} \rangle=\frac{1}{\sqrt{2}} \left(\vert \overline{0} \rangle + \vert \overline{1} \rangle\right).
Another way to understand logical gates is through their actions on the stabilizer group. Indeed, we can prove the following proposition:
Proposition 1: a unitary L is a logical gate if and only if it maps the stabilizer group \mathcal{S} to itself, i.e.
L^{\dagger} SL \in \mathcal{S} for all S \in \mathcal{S}.
Note that this is precisely the definition of the normalizer of the group \mathcal{S}, denoted \mathcal{N}(\mathcal{S}), and you will often find logical gates defined in the literature as elements of the normalizer of the stabilizer group. This proposition explains why those two definitions are equivalent, and proving it is a cute little exercise that I encourage you to try on your own before reading the solution at the end of this post.
Exercise 2: Prove Proposition 1 (solution)
Let’s apply this to the Steane code. For instance, let’s consider the operator H_L=H^{\otimes 7} consisting of applying a Hadamard gate on all the physical qubits:
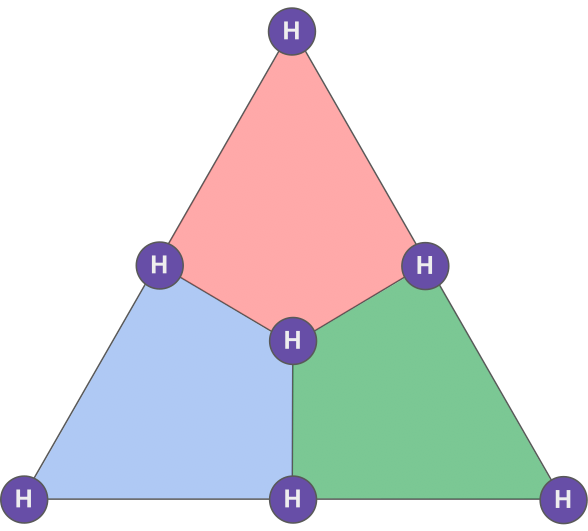
I claim that H_L is a logical gate. To show this, let’s use Proposition 1 and show that it maps stabilizers to stabilizers. Let’s pick an X plaquette, for instance the red one supported on qubits 1,2,3,4, that we will call S^X_r. Remember that H turns X into Z and Z into X, that is HXH=Z and HZH=X. Therefore:
\begin{aligned}
H_L S^X_r H_L
&= (H_1 \ldots H_7) X_1 X_2 X_3 X_4 (H_1 \ldots H_7) \\
&= (H_1 X_1 H_1) \ldots (H_4 X_4 H_4) H_5^2 H_6^2 H_7^2 \\
&= Z_1 Z_2 Z_3 Z_4 \\
& = S^Z_r
\end{aligned}where S^Z_r is the Z red plaquette. Therefore, H_L maps the X red plaquette to the Z red plaquette. The same reasoning can be applied to all the other X and Z plaquettes, showing that H_L maps stabilizers to stabilizers and is therefore a logical gate.
Note that we haven’t shown that H_L actually corresponds to a logical Hadamard, i.e. that it maps \vert \overline{0} \rangle to \vert \overline{+} \rangle and \vert \overline{1} \rangle to \vert \overline{-} \rangle. The easiest way to show that is by proving that H_L maps the logical X operator to the logical Z operator, and vice-versa.
The next step is therefore to get a grasp of the Pauli logical operators. But before that, feel free to try the following exercise to check your understanding of logical gates:
Exercise 3: Show that S_L=S^{\otimes 7} is a logical gate (solution)
Pauli logicals
An important family of logical gates are the Pauli logical operators (often abbreviated logical operators if the context is clear, or even just logicals).
As expected, those are the logical gates that belong to the Pauli group.
As two given Pauli operators can either commute or anticommute, Pauli logicals could either commute or anticommute with stabilizers.
However, if a Pauli logical anticommute with a stabilizer, that is SL=-LS, it means that L^{\dagger} S L = -S \notin \mathcal{S}, which contradicts the characterization of logical gates that we saw above. Therefore, Pauli logicals can be characterized by the following proposition:
Proposition 2: a Pauli operator P is a logical operator if and only if it commutes with all the stabilizers
Note that this is precisely the definition of the centralizer of the group \mathcal{S} in the Pauli group, denoted \mathcal{C}(\mathcal{S}). The difference between the normalizer and the centralizer is that if L \in \mathcal{N}(\mathcal{S}), LS=S'L for S, S' two stabilizers, while if L \in \mathcal{C}(\mathcal{S}), LS=SL. For Pauli operators, \mathcal{N}(\mathcal{S}) = \mathcal{C}(\mathcal{S}) and you will often find Pauli logicals defined with either normalizers or centralizers in the literature. Using either this characterization or the original definition, it is easy to show that the set \mathcal{L} of all Pauli logicals from a group, that is, the product of two logicals is itself a logical.
Finally, let’s define non-trivial logical operators (also known as logical errors) as elements of \mathcal{C}(\mathcal{S}) \backslash \mathcal{S}, or in other words, Pauli operators that commute with all the stabilizers but are not stabilizers themselves. We can now characterize the distance of a stabilizer code as the weight of the smallest logical error:
\begin{aligned}
d = \min_{L \in \mathcal{C}(\mathcal{S}) \backslash \mathcal{S}} |L|
\end{aligned}As usual, let’s apply what we’ve seen to the Steane code. I claim that the following operators, that we will call X_L and Z_L, are non-trivial logical operators of the code:
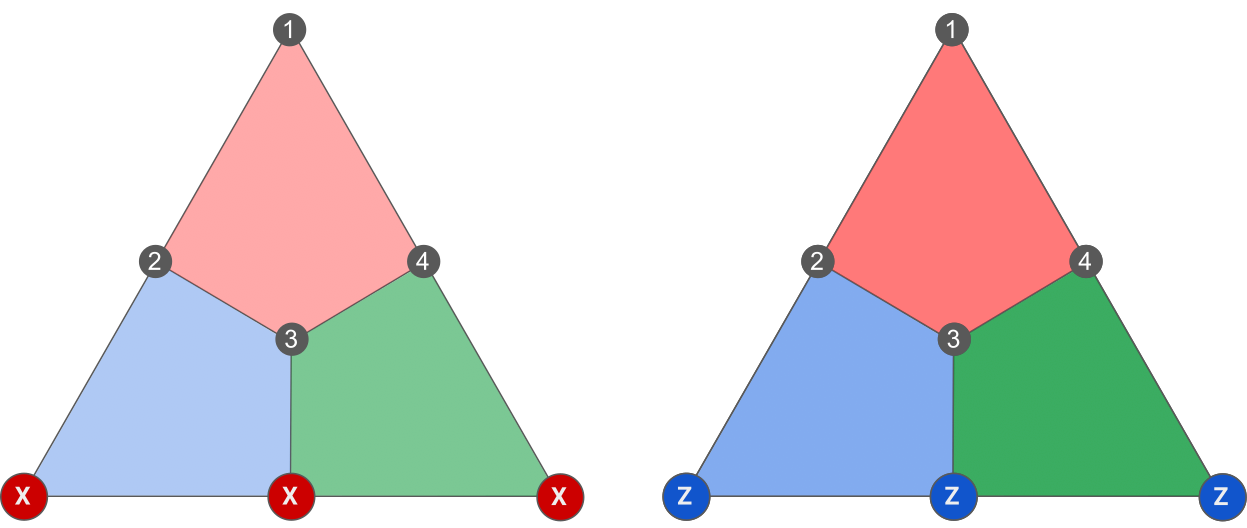
Indeed, it is easy to check that they commute with all the stabilizers, as they share either zero or two qubits with every plaquette. Moreover, by trying all the combinations of stabilizers, you can show that they don’t belong the stabilizer group, and are therefore non-trivial. By using a similar brute-force search, you can also show that they are the smallest non-trivial logical operators, thereby proving that the distance of the Steane code is d=3. This achieves the proof that the Steane code is a [[7,1,3]] code, as claimed in the previous post.
However, as discussed in the context of the Hadamard gate, we still haven’t shown that X_L and Z_L actually act as logical X and Z operators on the codespace. For that, we would need to show that X_L corresponds to a logical bit-flip and Z_L to a logical phase-flip, i.e. that they map respectively \vert 0 \rangle_L into \vert 1 \rangle_L and \vert + \rangle_L into \vert - \rangle_L. Alternatively, we could show that \vert 0 \rangle_L and \vert 1 \rangle_L are eigenstates of Z_L while \vert + \rangle_L and \vert - \rangle_L are eigenstates of X_L.
As it happens, this is just a matter of convention. There is no preferred \vert 0 \rangle_L state in the codespace, we have the freedom to pick any of the states and decide that it is going to be the zero state. For instance, for the repetition code, we decided that \vert 0 \rangle_L=\vert 000 \rangle, but we could have very much taken \vert 0 \rangle_L=\vert 111 \rangle or even \vert 0 \rangle_L=\frac{1}{\sqrt{2}} \left(\vert 000 \rangle+\vert 111 \rangle\right), as long as we keep track of it during the computation and when analyzing the measurements.
Therefore, as it is usually done with stabilizer codes, let’s define \vert 0 \rangle_L and \vert 1 \rangle_L as the two eigenstates of Z_L, and \vert + \rangle_L and \vert - \rangle_L as the two eigenstates of X_L. This is a valid choice since X_L and Z_L anticommute, and this also fixes the logical Y operator as Y_L=X_LZ_L. All the other logical gates are also fixed by how they transform those Pauli operators. For instance, you are now ready to prove that the logical gate H_L actually acts as a logical Hadamard gate.
Exercise 4: Show that H_L=H^{\otimes 7} acts as a logical Hadamard gate (solution)
(Hint: show that H_L X_L H_L=Z_L and H_L Z_L H_L=X_L)
Logical cosets
In the previous example, we saw one instance of logical X and Z operators.
However, there will often be multiple logical operators that act as a given Pauli.
Indeed, take a logical operator L \in \mathcal{L} and a stabilizer S \in \mathcal{S}. Then SL=LS is also a logical operator acting in the same way on the codespace:
\begin{aligned}
L S \vert \psi \rangle = L \vert \psi \rangle
\end{aligned}In other words, applying a stabilizer to a logical doesn’t change the way it acts on the codespace. We say that two logicals L and L' are equivalent if they only differ by a stabilizer, that is, if there exists S \in \mathcal{S} such that SL=L'. For instance, we have the following three equivalent logical X operators in the Steane code:
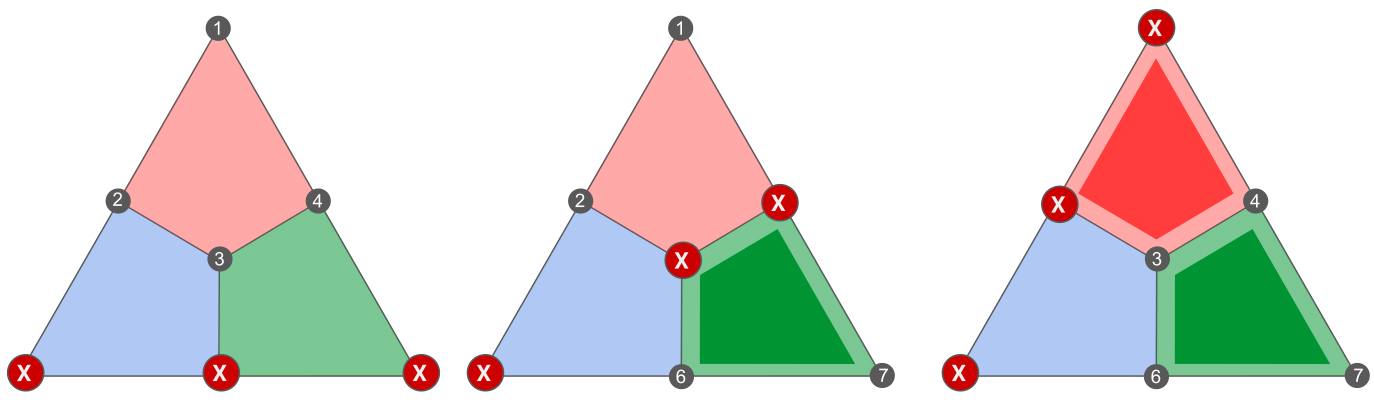
To go from the first one to the second one, we apply a green X plaquette. To go from the second one to the last one, we apply a red X plaquette.
Since all the equivalent logicals act in the same way on the codespace, it makes sense to group them together in some ways. The notion of equivalence classes is exactly what we need to formalize this idea.
An equivalence class, or coset, is a set of the form
\begin{aligned}
\bar{L}=L\mathcal{S}=\{ LS : S \in \mathcal{S} \}
\end{aligned}where L \in \mathcal{L} is any logical operator.
In other words, a coset is a set of equivalent logicals.
Any element P \in \bar{L} is called a representative of the coset \bar{L}.
For instance, any of the three X logicals of the figure above are representative of the coset \bar{X} of X logicals. Note that since the Steane code has only one qubit, all the X logicals are equivalent and there is only one coset of X logicals.
Let’s remember a few important properties of equivalence classes. First of all, they partition the set of logical operators, that is, they are all disjoint (i.e. have an empty intersection) and their union is the whole set. In the case of the Steane code, this can be written[^2]:
\begin{aligned}
\mathcal{L}=\bar{I} \cup \bar{X} \cup \bar{Y} \cup \bar{Z}
\end{aligned}If we had multiple logical qubits, we would have three different cosets \bar{X_i}, \bar{Y_i}, \bar{Z_i} for each logical qubit.
Secondly, the set of all the cosets form a group, which is called the quotient group of \mathcal{L} by \mathcal{S}, and denoted \mathcal{L} / \mathcal{S}. In this group, the multiplication between two cosets \bar{L}_1=L_1 \mathcal{S} and \bar{L}_2=L_2 \mathcal{S} is defined as L_1 L_2 \mathcal{S}, where L_1 and L_2 are two arbitrary representatives of \bar{L}_1 and \bar{L}_2. It is a nice exercise to check that the result does not depend on the choice of the two representatives. Moreover, you can check that the identity element of the group is \bar{I}=\mathcal{S}.
Finally, the quotient group can be generated by all the \bar{X}_i, \bar{Z}_i. This means that the number of logical qubits is exactly half the number of generators of \mathcal{L}/\mathcal{S}. This simple fact gives us a different way to count the number of logical qubits of a given stabilizer code, which will become extremely important when discussing topological quantum error correction in future posts.
Conclusion
In this post, we have introduced many crucial concepts to understand stabilizer codes. We have defined logical gates as operators that preserve the codespace, or equivalently, the stabilizer space. Those corresponds to elements of the normalizer of \mathcal{S}. In the specialize case of Pauli operators, we have seen that they correspond to elements of the centralizer, that is, elements that commute with all the stabilizers. We have seen that logical operations are highly degenerate in stabilizer codes, as multiplying a logical operator by a stabilizer gives the same operation on the codespace. We have therefore shown how to group equivalent logicals together within equivalent classes. We have learned how to compute the number of logical qubits in two different ways: either by counting the number m of generators of \mathcal{S} and using k=n-m, or by counting the number of generators of \mathcal{L} / \mathcal{S} and dividing by two. Finally, we have seen that the distance can be obtained by finding the minimum-weight logical operator. All those ideas have been illustrated using the Steane code, which we have proven to be a [[7,1,3]]-code.
In the next and last part of this trilogy, we will see how to formulate the stabilizer formalism in a more concrete way, using parity-check matrices in the binary symplectic format. This format, widely used in numerical implementations of quantum codes, will allow us to switch from group theory to linear algebra. We will express stabilizers and logicals as binary vectors, with commutation relations corresponding to a linear operation on those vectors. Using the notion of logical cosets that we have learned in this post, we will finally be able to formalize the decoding problem for quantum codes.
Solution of the exercises
Exercise 1: Let \Pi_{\mathcal{C}}=\frac{1}{2^m} (I+S_1)\ldots (I+S_m)
(a) Show that \Pi_{\mathcal{C}} is a projector onto the codespace, that is, \Pi_{\mathcal{C}} |\psi\rangle=|\psi\rangle if |\psi\rangle \in \mathcal{C}, and \Pi_{\mathcal{C}} |\psi\rangle=0 if |\psi\rangle \in \mathcal{C}^\perp.
(b) Show that we can rewrite this projector as \Pi_{\mathcal{C}}=\frac{1}{2^m}\sum_{S \in \mathcal{S}} S, where \mathcal{S} is the full stabilizer group.
(c) Show that \text{Tr}[\Pi_\mathcal{C}]=\text{dim}(\mathcal{C})
(d) Deduce that \text{dim}(\mathcal{C})=2^{n-m}
Correction:
(a) Let’s show that each operator \frac{1}{2}(I+S_i) is a projector onto the space stabilized by S_i. If |\psi\rangle is stabilized by S_i, we have \frac{1}{2}(I+S_i)|\psi\rangle=\frac{1}{2}|\psi\rangle+\frac{1}{2}S_i|\psi\rangle=\frac{1}{2}|\psi\rangle+\frac{1}{2}|\psi\rangle=|\psi\rangle. If |\psi\rangle is in the orthogonal complement of this space, it means that S_i|\psi\rangle=-|\psi\rangle, and therefore \frac{1}{2}(I+S_i)|\psi\rangle=\frac{1}{2}|\psi\rangle+\frac{1}{2}S_i|\psi\rangle=\frac{1}{2}|\psi\rangle-\frac{1}{2}|\psi\rangle=0. The product of those operators is therefore a projector onto the space stabilized by all the stabilizers.
(b) There are exactly 2^m elements in the group \mathcal{S}, each defined by the choice of the generators to include in the stabilizers. This is due to the independence of the generators, meaning that their products always defines a new stabilizer. When developing the expression of \Pi_\mathcal{C}, we therefore get all the elements of the stabilizer group exactly once in the sum.
(c) The eigenvalues of \Pi_{\mathcal{C}} are 1 and 0, with the multiplicity of 1 corresponding to the dimension of the codespace (since \Pi_{\mathcal{C}} projects onto the codespace). The trace is therefore exactly this dimension.
(d) Taking the trace on both sides, we get \text{dim}(\mathcal{C})=\frac{1}{2^m}\sum_{S \in \mathcal{S}} \text{Tr}[S]. Since all stabilizers are Paulis, their trace is zero except for the identity element, for which it is 2^n (the total dimension of the space). Therefore, the sum is equal to 2^n and we recover the desired formula.
(Back to section)
Exercise 2: Prove that a unitary L is a logical gate if and only if it maps the stabilizer group \mathcal{S} to itself, i.e.
L^{\dagger} SL \in \mathcal{S} for all S \in \mathcal{S}.
Correction: For the first direction, let’s suppose that L is a logical gate, i.e. L maps the codespace to itself.
For S \in \mathcal{S}, let’s show that LSL^{\dagger} \in \mathcal{S}, that is, LSL^{\dagger} \vert \psi \rangle = \vert \psi \rangle for all \vert \psi \rangle \in \mathcal{C}. For \vert \psi \rangle \in \mathcal{C}, L\vert \psi \rangle \in \mathcal{C} by assumption, so SL\vert \psi \rangle = L \vert \psi \rangle and L^{\dagger} S L \vert \psi \rangle = L^{\dagger} L \vert \psi \rangle = \vert \psi \rangle.
For the other direction, let’s suppose that L \in \mathcal{N}(\mathcal{S}), and let’s show that for a state \vert \psi \rangle \in \mathcal{C}, L \vert \psi \rangle \in \mathcal{C}. It comes down to showing SL \vert \psi \rangle = L \vert \psi \rangle for S \in \mathcal{S}. Since L^{\dagger} S L \in \mathcal{S} by assumption, there exists S' \in \mathcal{S} such that L^{\dagger} S L = S', or equivalently, SL = LS'. Therefore, SL\vert \psi \rangle = LS'\vert \psi \rangle = L \vert \psi \rangle.
(Back to section)
Exercise 3: Show that S_L=S^{\otimes 7} is a logical gate
Correction: Remember that the S gate turns X into Z and Z into itself.
Let’s pick any X plaquette. Applying S_L turns X^{\otimes 4} into Y^{\otimes 4}.
Since Y^{\otimes 4}=X^{\otimes 4} Z^{\otimes 4} (up to a phase), it is a product of stabilizers and therefore a stabilizer itself.
Moreover, S_L leaves Z plaquettes unchanged.
Thus, S_L maps stabilizers to stabilizers and forms a logical gate.
(Back to section)
Exercise 4: Show that H_L=H^{\otimes 7} acts as a logical Hadamard gate
(Hint: show that H_L X_L H_L=Z_L and H_L Z_L H_L=X_L)
Correction: Consider the logical X operator X_L=X^{\otimes 3} acting on qubits 5,6,7.
We get H_L X_L H_L = Z^{\otimes 3}=Z_L.
Using a similar reasoning, we can show that H_L Z_L H_L =X_L.
Thus, H_L acts as a logical Hadamard on the codespace.
(Back to section)
